Resolución de malla por KENELLY.

Análisis de circuitos I. Ecuaciones de Kenelly.

Bienvenido a esta serie de ejercicios en los cuales intentaré que aprendáis los conceptos del análisis de circuito de mallas mediante las ecuaciones de Kenelly.

Existen muchas formas de resolución de circuitos complejos al transformarlos en circuitos serie - paralelo cuya resolución es sencilla para el usuario usando la ley de Ohm.

Las ecuaciones de Kenelly transforman circuitos en "pi" (paralelo - serie), en circuitos en estrella (serie - paralelo), haciendo que el cálculo de la resistencia Thevenin sea más sencillo.

El punto de vista del circuito es fundamental. Ya que si en el circuito anterior quitamos la resistencia R3 de la malla inferior, la resolución del circuito es tan simple que se puede calcular por Ohm:

Por lo que la resolución del circuito es:

[(R1|| R2) + R4] || R5

Pero en un circuito con resistencia en todas las ramas como la mostrada en el primer circuito, éste método no funciona y hay que aplicar otros métodos como el del eslabón o Cramer entre otros. Y ahora vamos a ver las ecuaciones de Kenelly, que aplicarlas es muy sencillo de acuerdo a unas normas. 

ECUACIONES DE KENELLY.

El método de Kenelly consiste en convertir un circuito con varias resistencias en una configuración de estrella o de triángulo.

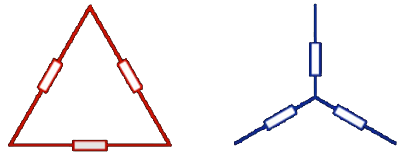
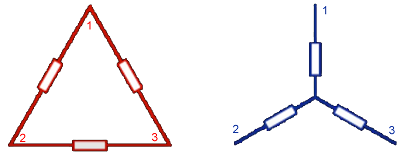
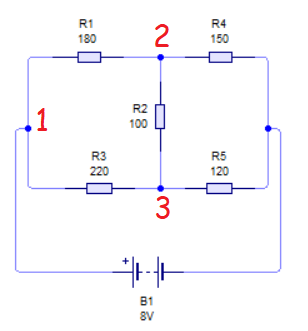
Para la transformación tenemos que numerar primero los elementos que entran en juego en el circuito. Se enumeran los vértices de ambas configuraciones como se ve en la siguiente imagen:

La numeración de los elementos es la misma en ambas configuraciones. Empezando por el extremo superior, la configuración de los números es hacia izquierda.

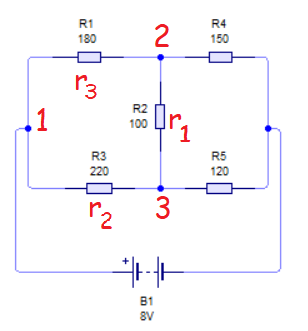
En cuanto a la numeración de las resistencias, en la estrella, las denominaremos por letras mayúsculas y su subíndice coincidirá con el número del vértice en que están conectadas. En el triángulo designaremos las resistencias en minúsculas y sus subíndices coincidirán con el número del vértice opuesto.

Y ahora para determinar la relación entre unas resistencias y otras hay que tener en cuenta qué valor de las resistencias medidas entre los terminales 1-2, 1-3 y 2-3, ha de ser igual en ambas configuraciones.

R₁ + R₂ = r₃(r₂ + r₁) ÷ r₃ + r₂ + r₁

R₁ + R₃ = r₂(r₁ + r₃) ÷ r₂ + r₁ + r₃

R₂ + R₃ = r₁(r₂ + r₃) ÷ r₁ + r₂ + r₃

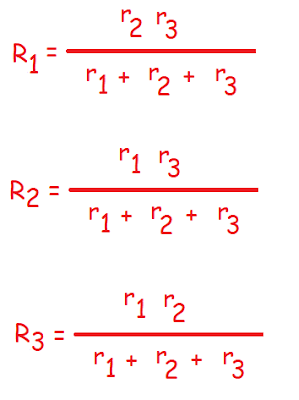
Operando estas ecuaciones nos queda las fórmulas relacionales para cada elemento.

Triángulo equivalente:

Estrella equivalente:

Así que ya con el circuito anterior resolvámoslo mediante Kenelly.

RESOLUCIÓN DE CIRCUITO.

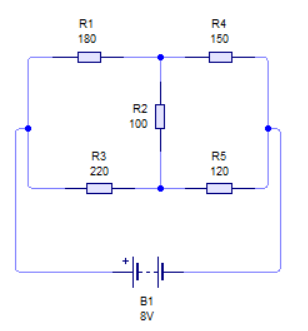
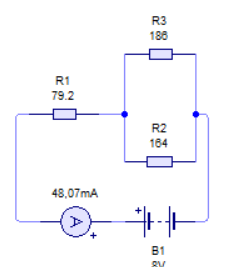
Partiendo del circuito siguiente.

Primero vamos a transformar la malla de la izquierda. Puedes ver que es un triángulo ya que las resistencias R1 y R3 se unen en el mismo terminal. Por eso, sabemos ya que la transformación será a estrella de dicho triángulo. Primero entonces, establecemos la numeración de sus terminales.

Lo siguiente es, identificar las resistencias en estrellas.

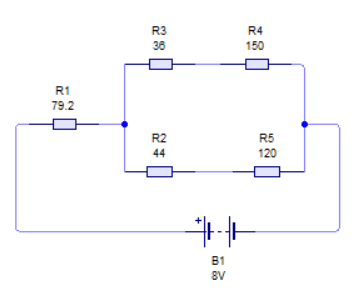
Y ahora simplemente hay que aplicar la fórmula de estrella equivalente, por lo que los valores que nos devuelven son los siguientes:

R₁ =39600 ÷ 500 = 79,2Ω

R₂ =22000 ÷ 500 = 44Ω

R₃ =18000 ÷ 500 = 36Ω

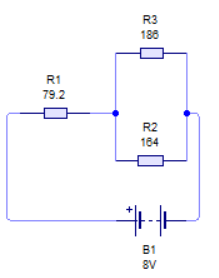
El circuito equivalente quedaría como ves en la imagen.

Ahora ya es más fácil de resolver, ¿verdad?

Eso te devuelve una resistencia total de 166,3Ω y una intensidad de corriente de 48mA.

Os dejo el vídeo de calculo de circuitos. Saludos.